Après avoir simulé des FFT avec Python et pylab, voyons comment les intégrer dans un FPGA réel de Xilinx.
Faire une FFT dans un FPGA est quelque chose qui n’est pas trivial. L’avantage, suivant la taille du FPGA, est de pouvoir en faire tourner plusieurs en parallèle pour accélérer le traitement. L’inconvénient étant le temps de développement qui est décuplé par rapport à une solution embarquée sur les habituels DSP ou microcontrôleurs.
Pour accélérer le développement, l’utilisation de modules fournis par les constructeurs est très tentante. Bien sûr, si on utilise la FFT d’un constructeur X, elle ne sera pas utilisable sur le FPGA du constructeur Y… Mais c’est de bonne guerre.
Plus gênant est la difficulté de simuler le module sur son PC pour valider l’algorithme que l’on souhaite mettre en œuvre.
C’est pour cela que Xilinx fournit un modèle C de sa FFT. Modèle que l’on peut utiliser gratuitement avec GCC.
Voyons voir comment mettre tout ça en œuvre.
Installation du modèle
Pour compiler le modèle il faut d’abord le générer à partir d’un projet Vivado. On crée donc un projet Vivado avec un FPGA cible et on instancie le bloc «Fast Fourrier Transform» dans l’«IP designer». Pour pouvoir générer le modèle il faut que les entrées/sorties soient connectées à quelques chose, dans notre cas nous nous contenterons d’exporter les ports.
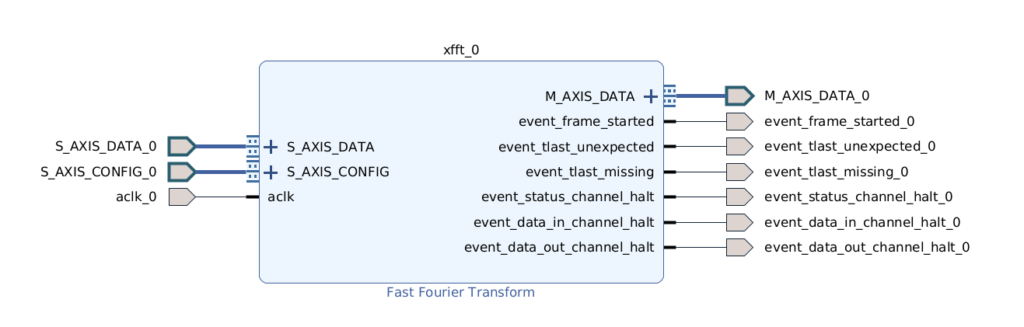
L’archive au format zip est générée dans le répertoire suivant :
test_fft/test_fft.gen/sources_1/bd/fft_test_design/ip/fft_test_design_xfft_0_0/cmodel/xfft_v9_1_bitacc_cmodel_lin64.zipArchive que l’on dézippera dans le répertoire de son choix :
$ unzip xfft_v9_1_bitacc_cmodel_lin64.zip
$ ls -l
gmp.h
libgmp.so.11
libIp_xfft_v9_1_bitacc_cmodel.so
make_xfft_v9_1_mex.m
run_bitacc_cmodel.c
run_xfft_v9_1_mex.m
xfft_v9_1_bitacc_cmodel.h
xfft_v9_1_bitacc_mex.cppet à laquelle nous ajouterons un fichier main() et un Makefile. Par contre ne rêvez pas, il n’y a pas les sources du modèle 😉 le modèle se trouve dans le fichier binaire de librairie libIp_xfft_v9_1_bitacc_cmodel.so
L’explication pour la compilation est donnée sur le site officiel. Avec g++ ça donne :
$ g++ -std=c++11 -I. -L. -lgmp -Wl,-rpath,. run_bitacc_cmodel.c -o run_fft -lIp_xfft_v9_1_bitacc_cmodelLa compilation génère un binaire nommé run_fft qu’il faut lancer en intégrant les librairies du répertoire courant pour le lien dynamique :
$ LD_LIBRARY_PATH=$$LD_LIBRARY_PATH:. ./run_fft
Running the C model...
Simulation completed successfully
Outputs from simulation are correct
$ Le résultat est relativement frustrant: certes il n’y a pas d’erreur, mais enfin bon … on n’est pas super avancé. On aimerait bien avoir de belles courbes et pouvoir admirer le résultat spectral de cette FFT !
Pour cela il va falloir se plonger dans le code «main()» et injecter son propre signal.
Plongée dans le code
Pour avoir la documentation du modèle on pourra bien sûr se référer à la documentation officiel, mais on peut également se plonger dans le header xfft_v9_1_bitacc_cmodel.h qui est bien commenté.
Le calcul est lancé avec la fonction xilinx_ip_xfft_v9_1_bitacc_simulate déclarée ainsi :
/**
* Simulate this bit-accurate C-Model.
*
* @param state Internal state of this C-Model. State
* may span multiple simulations.
* @param inputs Inputs to this C-Model.
* @param outputs Outputs from this C-Model.
*
* @returns Exit code Zero for SUCCESS, Non-zero otherwise.
*/
Ip_xilinx_ip_xfft_v9_1_DLL
int xilinx_ip_xfft_v9_1_bitacc_simulate
(
struct xilinx_ip_xfft_v9_1_state* state,
struct xilinx_ip_xfft_v9_1_inputs inputs,
struct xilinx_ip_xfft_v9_1_outputs* outputs
);L’état est créé avec la fonction xilinx_ip_xfft_v9_1_create_state() et la structure d’entrée (inputs) possède un tableau de double pour la partie imaginaire et un tableau de double pour la partie réelle. La taille de la FFT étant donnée en 2^n par l’attribut nfft.
struct xilinx_ip_xfft_v9_1_inputs
{
int nfft; //@- log2(point size)
double* xn_re; //@- Input data (real)
int xn_re_size;
double* xn_im; //@- Input data (imaginary)
int xn_im_size;
int* scaling_sch; //@- Scaling schedule
int scaling_sch_size;
int direction; //@- Transform direction
}; // end xilinx_ip_xfft_v9_1_inputsLa structure de sortie est encore plus simple :
struct xilinx_ip_xfft_v9_1_outputs
{
double* xk_re; //@- Output data (real)
int xk_re_size;
double* xk_im; //@- Output data (imaginary)
int xk_im_size;
int blk_exp; //@- Block exponent
int overflow; //@- Overflow occurred
}; // xilinx_ip_xfft_v9_1_outputsDans l’exemple donnée, la partie imaginaire est fixée à 0 sur les 1024 échantillons et la partie réel à 0.5.
// Create input data frame: constant data
double constant_input = 0.5;
int i;
for (i=0; i<samples; i++) {
xn_re[i] = constant_input;
xn_im[i] = 0.0;
}Si le signal est constant, en toute logique seule la fréquence continue (0Hz) doit être différente de 0. C’est ce qui est vérifié après avoir effectué le calcul :
// Check xk_re data: only xk_re[0] should be non-zero
double expected_xk_re_0;
if (C_HAS_SCALING == 0) {
expected_xk_re_0 = constant_input * (1 << C_NFFT_MAX);
} else {
expected_xk_re_0 = constant_input;
}
if (xk_re[0] != expected_xk_re_0) {
cerr << "ERROR:" << channel_text << " xk_re[0] is incorrect: expected " << expected_xk_re_0 << ", actual " << xk_re[0] << endl;
ok = false;
}
for (i=1; i<samples; i++) {
if (xk_re[i] != 0.0) {
cerr << "ERROR:" << channel_text << " xk_re[" << i << "] is incorrect: expected " << 0.0 << ", actual " << xk_re[i] << endl;
ok = false;
}
}
// Check xk_im data: all values should be zero
for (i=1; i<samples; i++) {
if (xk_im[i] != 0.0) {
cerr << "ERROR:" << channel_text << " xk_im[" << i << "] is incorrect: expected " << 0.0 << ", actual " << xk_im[i] << endl;
ok = false;
}
}Transformée de wavelet
Tout ceci n’est pas très parlant pour le moment, testons maintenant le modèle sur la «wavelet» générée à partir d’un script python. Le script permettant de générer le signal et de l’écrire dans un fichier *.txt se trouve dans le répertoire cmodel du dépot github.
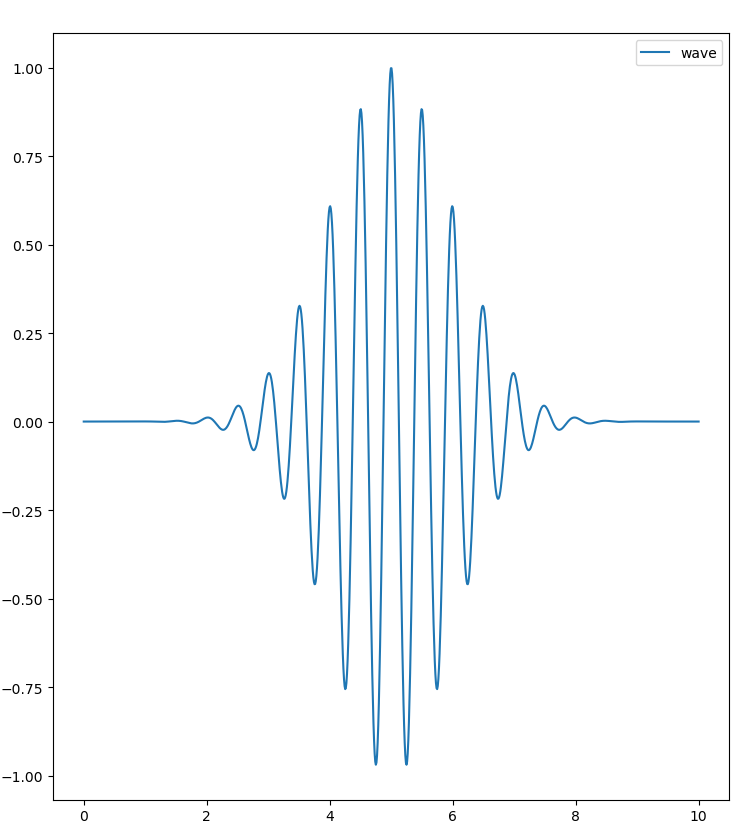
Le script génère un fichier ysig.txt avec toutes les valeurs flottantes écrites en ASCII. On va ensuite relire le fichier avec le programme C++ :
// Read input data from file ysig.txt
std::ifstream yfile; yfile.open("ysig.txt");
if(!yfile.is_open()){
perror("Open error");
exit(EXIT_FAILURE);
}
string line;
int i=0;
while(getline(yfile, line)){
xn_re[i] = stof(line);
cout << stof(line) << endl;
xn_im[i] = 0.0;
i++;
}Le programme écrira le résultat sous dans le fichier xfft_out.txt une fois le résultat calculé:
// save outputs in xfft_out.txt
std::ofstream outfile; outfile.open("xfft_out.txt");
if(outputs.xk_re_size != outputs.xk_im_size){
printf("Error imaginary part size is not equal to real part");
}
for(int i=0; i < outputs.xk_re_size; i++){
outfile << outputs.xk_re[i] << ", " << outputs.xk_im[i] << endl;
}
Fichier que l’on relira pour l’afficher au moyen du script python plot_fft.py
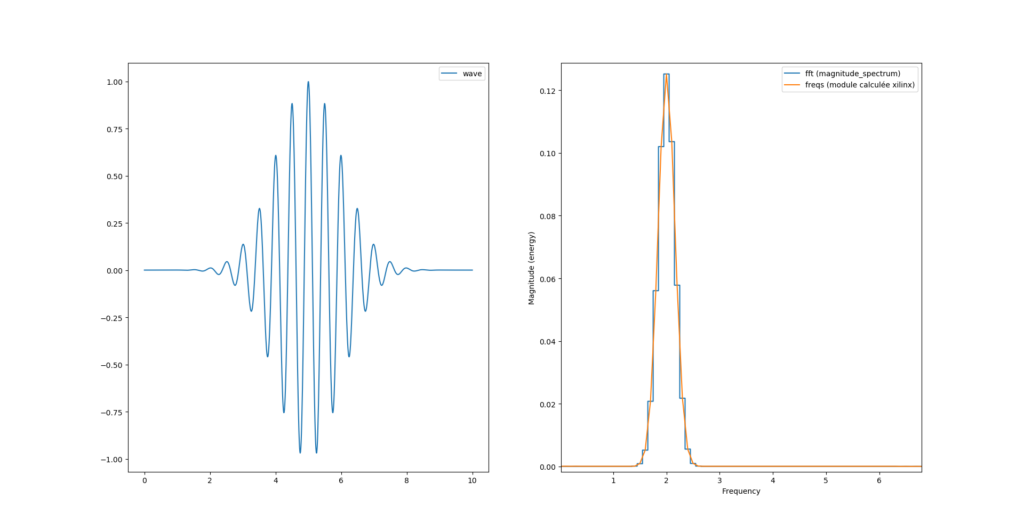
Et nous avons la bonne surprise d’obtenir le même spectre du module qu’avec la fonction de pylab.
On peut maintenant jouer avec les paramètres du module Xilinx et affiner notre modèle de simulation avant de le synthétiser dans un FPGA (de chez Xilinx évidement 😉