Quand on utilise la suite symbiflow pour synthétiser un projet sur le eFPGA (pp3) de la quickfeather on tombe sur des nom étranges de cellule logique.
Circuit Statistics:
Blocks: 65
.output : 3
ASSP : 1
BIDIR_CELL: 3
C_FRAG : 7
F_FRAG : 1
GND : 1
Q_FRAG : 22
T_FRAG : 26
VCC : 1À quoi correspondent les blocks C_FRAG, T_FRAG, ASSP, … ?
Et il est assez compliqué de trouver la documentation correspondante. On retrouve une description en Verilog de ces blocs dans le répertoire suivant du SDK :
$ ls qorc-sdk/fpga_toolchain_install/v1.3.1/quicklogic-arch-defs/share/techmaps/quicklogic/pp3/techmap/
cells_map.v cells_sim.v lut2tomux2.v lut2tomux4.v lut3tomux2.v mux4tomux2.v mux8tomux2.vEt plus particulièrement dans le fichier source cells_map.v qui semble décrire au moyen de plusieurs «FRAG»ment de module le schéma de la figure 36 de la datasheet (page 60).
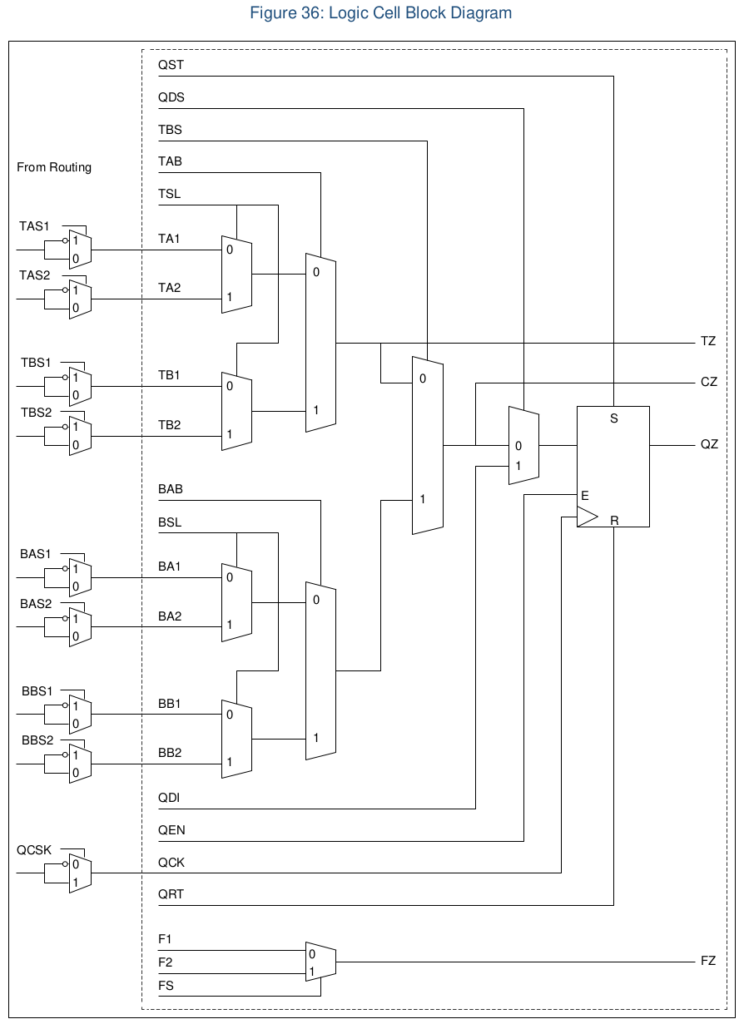
En lisant le code du fichier cells_sim.v on trouve les relations suivantes dans le schéma.
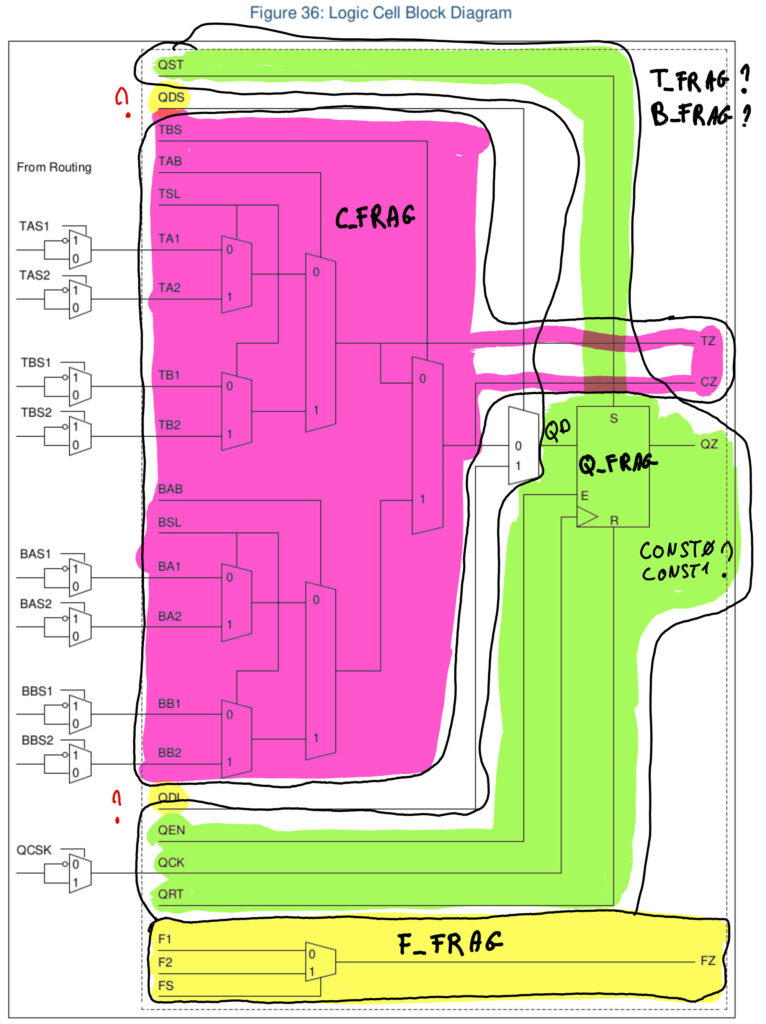
Les nom de signaux QDI et QDS ne se trouvent pas dans le fichier source, ils sont liés au multiplexeur situé devant la bascule D Q_FRAG et semble correspondre aux constantes CONST0 et CONST1 que l’on trouve dans les sources.
Pour les fragments T_FRAG et B_FRAG c’est moins clair en se servant du nom des signaux mais ils semblent liés à des bits de configuration que l’on trouve à gauche du schéma (BAS, BBS, TAS, …)
On imagine aisément que le FRAG correspond à Fragment mais les lettres préfixes sont moins claires.
Si on fait la liste des noms de block donnés au début on a
- ASSP: celui là est plus clair. C’est le bloc qui assure la communication avec le microcontrolleur, avec les différents signaux de bus (Wishbone, SPI, …) ainsi que l’horloge, et autres signaux de contrôles.
- BIDIR_CELL: Ça c’est un buffer d’entrée sortie `iopad`
- C_FRAG: Cet enchevêtrement de multiplexeurs ressemble fort à une LUT avec une sortie retenue (C pour Carry).
- F_FRAG: Là on a affaire à un simple multiplexeur deux entrées, pour faciliter le routage (routage rapide ?)
- GND: bon bin … la masse quoi (mais qu’est-ce que ça vient faire là ?)
- Q_FRAG: Q pour la sortie de la bascule D Flip flop.
- T_FRAG: ?
- VCC: L’alim, …
- B_FRAG: celui là n’est pas dans le rapport de routage mais se trouve dans le code verilog, il ressemble à T_FRAG.
Tout cela n’est pas parfaitement claire.
Et surtout on aurait aimé avoir un schéma d’architecture du eFPGA comme on peut le voir dans les datasheet des autres constructeur. Avec l’alignement des différentes cellule et une description graphique des entrées sorties.
C’était juste une prise de note (susceptible d’évoluer comme d’habitude) pour tenter de comprendre ce FPGA à la documentation pas très claire.
[Edit 2024/01/19]
J’ai eu des réponses sur le site officiel \o/ Il y a plus de détails du coup. Je vais pouvoir continuer mes investigations.